SAT Math – Algebra
Graphs of Linear Equations & Functions
Mastering visual interpretation and graphical analysis of linear relationships
Graph interpretation questions appear on every SAT Math section, testing your ability to extract information from visual representations of linear equations. These questions require you to identify slopes, intercepts, and equations directly from graphs—skills that combine algebraic understanding with visual reasoning.
Success with linear graphs demands fluency in multiple representations: moving seamlessly between equations, tables, graphs, and verbal descriptions. This guide provides systematic approaches to reading graphs, determining equations, and avoiding the common traps that catch test-takers under time pressure.
Understanding Linear Graphs
What is a Linear Graph?
A linear graph is the visual representation of a linear equation, appearing as a straight line on the coordinate plane. Every point \((x, y)\) on the line satisfies the equation.
- Always forms a straight line (never curves)
- Has constant slope throughout
- Can be described by equation \(y = mx + b\)
- Extends infinitely in both directions
Essential Graph Components
- Slope (m): The steepness and direction of the line; found by \(\frac{\text{rise}}{\text{run}}\)
- Y-intercept (b): Where the line crosses the y-axis; the point \((0, b)\)
- X-intercept: Where the line crosses the x-axis; found when \(y = 0\)
- Direction: Lines with positive slopes rise left to right; negative slopes fall
Special Linear Graphs
Horizontal lines: Form \(y = c\) (slope = 0)
Vertical lines: Form \(x = c\) (undefined slope)
Lines through origin: Form \(y = mx\) (no y-intercept term)
Essential Formulas for Reading Graphs
Slope Formula (From Graph)
\(m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\text{rise}}{\text{run}} = \frac{\text{vertical change}}{\text{horizontal change}}\)
Choose any two clear points on the line, then count the vertical change and horizontal change between them.
Writing Equation from Graph
\(y = mx + b\)
Step 1: Identify y-intercept \(b\) (where line crosses y-axis)
Step 2: Calculate slope \(m\) using two points
Step 3: Substitute into \(y = mx + b\)
Finding Intercepts
Y-intercept: Point where \(x = 0\); look where line crosses y-axis
X-intercept: Point where \(y = 0\); look where line crosses x-axis
Recognizing Slope by Direction
Positive slope (\(m > 0\)):
Line rises from left to right ↗
Negative slope (\(m < 0\)):
Line falls from left to right ↘
Zero slope (\(m = 0\)):
Horizontal line →
Undefined slope:
Vertical line ↑
Common Pitfalls & Expert Tips
❌ Miscounting rise and run
Always count carefully on graph paper. A common error is counting 3 units when it's actually 4. Use the grid lines, not approximations.
❌ Confusing x-intercept and y-intercept
Y-intercept is where the line crosses the y-axis (vertical axis), not the x-axis. The point is \((0, b)\), not \((b, 0)\).
❌ Ignoring axis scales
Not all graphs use scale 1. If each square represents 2 units, a rise of 2 squares = rise of 4 units. Always check the scale!
❌ Reversing rise and run
Slope is \(\frac{\text{rise}}{\text{run}}\), not \(\frac{\text{run}}{\text{rise}}\). Rise is vertical (y-direction), run is horizontal (x-direction).
✓ Expert Tip: Use clear lattice points
Choose points where the line clearly passes through grid intersections. Avoid estimating between grid lines—this introduces errors.
✓ Expert Tip: Check your slope sign
If the line goes upward left to right, slope is positive. If it goes downward, slope is negative. This quick visual check catches sign errors.
✓ Expert Tip: Verify with a second point
After finding your equation, plug in a visible point from the graph to confirm it works. This catches calculation mistakes.
Fully Worked SAT-Style Examples
A line passes through points \((2, 1)\) and \((6, 5)\) on a graph. What is the slope of the line?
Visualize: Starting at point (2, 1), moving to (6, 5) requires moving right 4 units and up 4 units.
Solution:
Step 1: Identify the two points
Point 1: \((x_1, y_1) = (2, 1)\)
Point 2: \((x_2, y_2) = (6, 5)\)
Step 2: Apply the slope formula
\(m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{5 - 1}{6 - 2} = \frac{4}{4} = 1\)
Interpretation:
A slope of 1 means that for every 1 unit you move right, the line moves up 1 unit.
This is a 45° angle line rising left to right.
Answer: The slope is \(m = 1\)
A line crosses the y-axis at \((0, -3)\) and passes through point \((4, 5)\). Write the equation of the line in slope-intercept form.
Solution:
Step 1: Identify the y-intercept
The line crosses the y-axis at \((0, -3)\)
Therefore, \(b = -3\)
Step 2: Calculate the slope using the two points
Points: \((0, -3)\) and \((4, 5)\)
\(m = \frac{5 - (-3)}{4 - 0} = \frac{5 + 3}{4} = \frac{8}{4} = 2\)
Step 3: Write the equation using \(y = mx + b\)
With \(m = 2\) and \(b = -3\):
\(y = 2x - 3\)
Verification:
Check with point \((4, 5)\): \(y = 2(4) - 3 = 8 - 3 = 5\) ✓
Check with point \((0, -3)\): \(y = 2(0) - 3 = -3\) ✓
Answer: \(y = 2x - 3\)
A line passes through points \((1, 8)\) and \((5, 0)\). What is the slope of this line, and what does the slope tell us about the line's direction?
Solution:
Step 1: Calculate the slope
Using points \((1, 8)\) and \((5, 0)\):
\(m = \frac{0 - 8}{5 - 1} = \frac{-8}{4} = -2\)
Step 2: Interpret the negative slope
A slope of \(-2\) means:
• For every 1 unit you move right, the line moves down 2 units
• The line descends from left to right
• The line has a negative (downward) direction
Visual Check:
Starting point: \((1, 8)\) is higher up
Ending point: \((5, 0)\) is lower down
The line indeed falls as we move left to right ✓
Answer: The slope is \(m = -2\)
The negative slope indicates the line descends from left to right.
The equation of a line is \(y = -\frac{1}{2}x + 4\). Find both the x-intercept and y-intercept of this line.
Solution:
Finding the Y-Intercept:
The y-intercept occurs when \(x = 0\)
From the equation \(y = -\frac{1}{2}x + 4\), the constant term is the y-intercept:
\(b = 4\)
Y-intercept: \((0, 4)\)
Finding the X-Intercept:
The x-intercept occurs when \(y = 0\)
Set \(y = 0\) and solve for \(x\):
\(0 = -\frac{1}{2}x + 4\)
\(\frac{1}{2}x = 4\)
\(x = 8\)
X-intercept: \((8, 0)\)
Graph Interpretation:
The line crosses the y-axis at height 4
The line crosses the x-axis at position 8
With negative slope, line falls from (0, 4) to (8, 0)
Answer: Y-intercept: \((0, 4)\); X-intercept: \((8, 0)\)
A line passes through points \((2, 5)\) and \((7, 5)\). What is the equation of this line?
Solution:
Step 1: Notice the pattern in the points
Both points have the same y-coordinate: \(y = 5\)
This indicates a horizontal line
Step 2: Calculate the slope (to confirm)
\(m = \frac{5 - 5}{7 - 2} = \frac{0}{5} = 0\)
A slope of 0 confirms this is a horizontal line
Step 3: Write the equation
For horizontal lines, the equation is simply:
\(y = 5\)
This means y always equals 5, regardless of x-value
Key Insight:
Horizontal lines have slope = 0
They are parallel to the x-axis
Equation form: \(y = c\) where \(c\) is a constant
Answer: \(y = 5\)
A line on a graph has a y-intercept of \(-2\) and a slope of \(\frac{3}{4}\). Which equation represents this line?
Answer choices:
A) \(y = \frac{3}{4}x + 2\)
B) \(y = \frac{3}{4}x - 2\)
C) \(y = -2x + \frac{3}{4}\)
D) \(y = \frac{4}{3}x - 2\)
Solution:
Step 1: Recall slope-intercept form
The general form is \(y = mx + b\)
Where \(m\) = slope and \(b\) = y-intercept
Step 2: Substitute the given values
Slope \(m = \frac{3}{4}\)
Y-intercept \(b = -2\)
\(y = \frac{3}{4}x + (-2)\) which simplifies to \(y = \frac{3}{4}x - 2\)
Step 3: Eliminate wrong answers
• Choice A has \(+2\), but y-intercept should be \(-2\) ✗
• Choice B has correct slope and intercept ✓
• Choice C has slope and intercept reversed ✗
• Choice D has wrong slope (\(\frac{4}{3}\) instead of \(\frac{3}{4}\)) ✗
Answer: B) \(y = \frac{3}{4}x - 2\)
A line passes through the origin \((0, 0)\) and the point \((3, -6)\). What is the equation of this line?
Solution:
Step 1: Identify the y-intercept
Since the line passes through the origin \((0, 0)\), the y-intercept is \(b = 0\)
Step 2: Calculate the slope
Using points \((0, 0)\) and \((3, -6)\):
\(m = \frac{-6 - 0}{3 - 0} = \frac{-6}{3} = -2\)
Step 3: Write the equation
Using \(y = mx + b\) with \(m = -2\) and \(b = 0\):
\(y = -2x + 0\) which simplifies to \(y = -2x\)
Key Concept:
Lines through the origin have the form \(y = mx\) (no constant term)
These represent proportional relationships
When \(x = 0\), \(y\) must also equal 0
Answer: \(y = -2x\)
Line A has equation \(y = 3x + 1\). Line B passes through points \((0, -2)\) and \((2, 4)\). Which line has a greater slope?
Solution:
Step 1: Find the slope of Line A
From the equation \(y = 3x + 1\), the slope is the coefficient of \(x\):
Slope of Line A: \(m_A = 3\)
Step 2: Calculate the slope of Line B
Using points \((0, -2)\) and \((2, 4)\):
\(m_B = \frac{4 - (-2)}{2 - 0} = \frac{4 + 2}{2} = \frac{6}{2} = 3\)
Slope of Line B: \(m_B = 3\)
Step 3: Compare the slopes
\(m_A = 3\) and \(m_B = 3\)
The slopes are equal!
Important Insight:
Lines with equal slopes are parallel
Line A: \(y = 3x + 1\) has y-intercept of 1
Line B has y-intercept of -2 (passes through \((0, -2)\))
These lines are parallel but not identical
Answer: Neither line has a greater slope; they have equal slopes of 3 and are parallel.
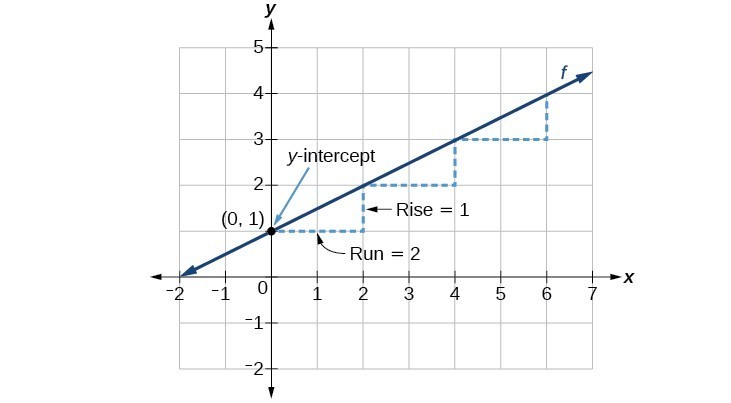
A line passes through \((0, 1)\) and \((6, 3)\). Write the equation of the line in slope-intercept form.
Solution:
Step 1: Identify the y-intercept
The line passes through \((0, 1)\), so \(b = 1\)
Step 2: Calculate the slope
Using points \((0, 1)\) and \((6, 3)\):
\(m = \frac{3 - 1}{6 - 0} = \frac{2}{6} = \frac{1}{3}\)
Always simplify fractions!
Step 3: Write the equation
\(y = \frac{1}{3}x + 1\)
Understanding the Slope:
A slope of \(\frac{1}{3}\) means:
• For every 3 units you move right, the line rises 1 unit
• This is a gentle upward slope
• Verification: At \(x = 6\), \(y = \frac{1}{3}(6) + 1 = 2 + 1 = 3\) ✓
Answer: \(y = \frac{1}{3}x + 1\)
The graph of line \(L\) in the xy-plane passes through \((-3, -1)\) and \((3, 5)\). Line \(M\) is parallel to line \(L\) and has a y-intercept of 2. What is the equation of line \(M\)?
Solution:
Step 1: Find the slope of line \(L\)
Using points \((-3, -1)\) and \((3, 5)\):
\(m_L = \frac{5 - (-1)}{3 - (-3)} = \frac{5 + 1}{3 + 3} = \frac{6}{6} = 1\)
Step 2: Use the parallel line property
Key fact: Parallel lines have identical slopes
Since line \(M\) is parallel to line \(L\):
\(m_M = m_L = 1\)
Step 3: Use the given y-intercept for line \(M\)
We're told line \(M\) has y-intercept of 2, so \(b = 2\)
Step 4: Write the equation of line \(M\)
Using \(y = mx + b\) with \(m = 1\) and \(b = 2\):
\(y = 1x + 2\) or simply \(y = x + 2\)
Key SAT Concept:
Parallel lines: Same slope, different y-intercepts
Line \(L\): \(y = x - 2\) (you can verify this with the points)
Line \(M\): \(y = x + 2\)
Both have slope 1, but different intercepts → parallel!
Answer: \(y = x + 2\)
Quick Reference: Reading Graphs
| Feature | How to Find on Graph | What It Tells You |
|---|---|---|
| Y-Intercept | Where line crosses y-axis (vertical axis) | Starting value when \(x = 0\) |
| X-Intercept | Where line crosses x-axis (horizontal axis) | Value of \(x\) when \(y = 0\) |
| Slope | Count rise/run between two clear points | Rate of change; steepness & direction |
| Direction | Rising left→right = positive; falling = negative | Sign of slope (+ or −) |
| Steepness | Vertical lines steepest; horizontal flattest | Absolute value of slope |
SAT Graph Strategy Guide
1. Always Check the Scale First
Before calculating anything, look at the axis labels. Each grid square might represent 1, 2, 5, or other values. Missing this causes most graph errors.
2. Use Lattice Points (Grid Intersections)
Choose points where the line clearly passes through grid intersections. Never estimate or guess between grid lines—this introduces unnecessary errors.
3. Verify Your Equation with a Test Point
After finding an equation, plug in a visible point from the graph to confirm it works. This catches arithmetic mistakes and wrong slope calculations.
4. Remember: Slope = Rise/Run (Not Run/Rise)
The vertical change (rise) goes in the numerator; horizontal change (run) in the denominator. This is probably the most reversed formula on the SAT.
5. Visual Check: Does Your Answer Make Sense?
If the graph shows a line rising steeply, your slope should be a large positive number. If it's barely rising, slope should be a small positive fraction. Use your eyes!
Special Cases to Master
Horizontal Lines
Form: \(y = c\) (constant)
Slope: 0
Example: \(y = 5\) is a horizontal line through all points where \(y = 5\)
Vertical Lines
Form: \(x = c\) (constant)
Slope: Undefined
Example: \(x = -2\) is a vertical line through all points where \(x = -2\)
Parallel Lines
Property: Same slope, different y-intercepts
Example: \(y = 2x + 3\) and \(y = 2x - 1\) are parallel (both have \(m = 2\))
Perpendicular Lines
Property: Slopes are negative reciprocals
Example: \(y = \frac{2}{3}x + 1\) and \(y = -\frac{3}{2}x + 4\) are perpendicular
Visual Fluency = SAT Success
Graph interpretation is one of the highest-yield skills for SAT Math. Every linear function can be represented as an equation, a table, a graph, or a verbal description—and the SAT tests your ability to move fluently between all four. Master the visual representation, and you unlock a powerful tool for checking your algebraic work, verifying solutions quickly, and developing intuition that speeds you through test day. The strategies in this guide aren't just for graphs—they're thinking tools that strengthen your entire mathematical foundation.